Long & Short Mean Reversion Machine Learning
Is it really possible to get over 40% annual returns over the past 10 years trading an ML-based mean reversion model?
The idea
"There is no magic in magic; it's all in the details.” Walt Disney.
As most creative people are, I'm a huge fan of Walt Disney and his attention to detail. One of the most famous stories about his attention to detail involves a seemingly small problem with light bulbs on Main Street, U.S.A., in Disneyland.
When Disneyland was being constructed, Walt Disney was deeply involved in every aspect of its design. Main Street, U.S.A., was designed to evoke the charm of a small American town from the early 20th century, with every detail meticulously planned. However, one particular problem arose during the installation of light bulbs on one of the marquees in the park.
The marquee had a row of alternating red and white light bulbs, but when the design team finished placing the bulbs, they found that they ended up with two bulbs of the same color next to each other. This imbalance bothered Disney, as it disrupted the visual harmony he envisioned for the park. The team was unsure how to solve the issue without disrupting the pattern of alternating colors.
Instead of accepting this small imperfection, Walt Disney insisted on a creative solution. He suggested that they paint one of the bulbs half red and half white. This way, it would seamlessly blend into the alternating pattern and maintain the visual flow that Disney was so intent on achieving.
This simple yet ingenious solution perfectly encapsulates Walt Disney's commitment to perfection and his belief that even the smallest details matter. He understood that while most guests might not consciously notice something as minor as two adjacent light bulbs being the same color, the overall experience would be subtly enhanced by the attention to detail.
This week, we are going to make 4 improvements to last week's Machine Learning and the Probability of Bouncing Back strategy:
First, we will fix a not-so-obvious bug that introduced bias into last week's strategy simulation, making the results better than what they should be;
Then, we will improve the process of gathering data used to train the model;
Next, we will re-train the long model, train the short model, and trade both in parallel;
Finally, we will add a regime filter based on VIX to reduce the drawdowns.
All the improvements involve attention to detail, which is extremely important in quantitative trading.
Even if you are not trading a system like the one I will describe here, there are some interesting insights and ideas worth considering. Let's get started.
Two types of biases: obvious vs. subtle
The first sign that something is not right usually comes when I see results that are too good to be true. Intuitively, I knew something was probably off (thus, I wrote the article's subtitle as a question, not as a statement), but I decided to share it anyway and look for the error later.
During this week, while I was reviewing the production code for this strategy, I found a potential error.
In my view, there are 2 types of biases:
A) The obvious types
Survivorship bias and selection bias are obvious:
If we pick a basket of stocks today based on any index (let's say, S&P 500), go back in time, and trade this fixed basket throughout history, we will obviously get an amazing backtest result.
If we test multiple strategies and varying parameters and then cherry-pick the best one, we will again obviously get an amazing backtest result.
However, in both cases, the results will be impossible to repeat in real life. First, we could never have predicted years ago which companies would be included in an index such as the S&P 500. Second, cherry-picking the best run out of hundreds of trials leads to results that are certainly due to pure luck - not statistically significant.
These biases are easy to spot and avoid. They are obvious. Unfortunately, they are not the only type.
B) The subtle types
Let's imagine that instead of being restricted to a certain index, we want to trade all stocks that meet certain liquidity criteria (e.g., the capital allocated to the trade does not exceed 5% of the stock's ADV).
Using a data provider such as Norgate Data, that's something simple to do: we just retrieve all symbols from the US Equities Listed and Delisted databases (~32K symbols), and we are good to go.
To reduce the number of symbols and make the computation faster, instead of getting all symbols from the US Equities Listed and Delisted databases, we could get all symbols from the Russell 3000 Current and Past watchlist (~12K symbols). This watchlist includes any symbol that has ever been a part of the Russell 3000 index at any point in time. That is a valid proxy, right?
Unfortunately, this little approximation includes a subtle bias (which is not survivorship bias nor selection bias). Let me explain.
Imagine the backtest is back in 2017, and it has all the symbols that have ever been a part of the Russell 3000 index at any point in time from 1998 to 2024:
The system has all delisted symbols, so it is survivorship-bias free;
The system might choose to trade symbols that have never been part of Russell 3000 up until that point in time - and there's nothing wrong with that, as we want to trade symbols in a universe not restricted to any index;
However, the only symbols that have never been part of Russell 3000 up to that point in time and are available to trade are symbols that will for sure be a part of Russell 3000 in the future! Such a system will never consider stocks that have never been part of Russell 3000 up to that point in time AND won't ever be part of it. This small, subtle detail introduces a bias (which is neither survivorship bias nor selection bias, at least in its most common form).
I think this might be called a “subtle selection bias”: although it is not selection bias in its most common form, it's some sort of bias that arises from the way the data is selected, leading to skewed results.
Why did this happen, and how could we fix it?
There are two possible solutions to our problem:
Restrict ourselves to trade only Russell 3000 stocks (the default behavior of any backtesting software);
Create a universe of tradable instruments based on the US Equities Listed and Delisted databases, not using any indices to help in its construction.
Both solutions are simple. The first one is easier to implement. We will go with that.
Most backtesting software, including mine, defaults to trading only symbols that belong to a certain index, current and past. This addresses the obvious survivorship bias and liquidity problems out of the box and simplifies the process.
The problem comes when we deviate from the default patterns and do not pay enough attention to detail. As I wanted more data to train the ML models, I decided to gather all available symbols. Then, I decided to simplify that choice by using all stocks that have ever been part of Russell 3000 as a proxy. This last decision introduced bias.
Improving the process of gathering data used to train the model
Another detail we overlooked while training the model has to do with how we gathered data for each symbol.
Once we defined the universe—all stocks that have ever been part of the Russell 3000 index—we gathered ALL the price action data for all symbols and computed the features. To highlight: we got all the price history for every stock. This could also be improved.
Instead of considering all history from every symbol in the universe, now we considered only the history when the symbol was part of the Russell 3000 index. Here's why:
First, for the features that use cross-sectional standardization, if we don't make this consideration, we potentially add an even more subtle selection bias (just reflect a bit, and you'll understand what I'm talking about);
Second, the period before a symbol was minimally liquid enough to be a part of Russell 3000 (or the period after it loses its liquidity to be removed from the index, for those stocks that get removed) has data that is most likely confusing the model instead of helping it improve its accuracy. That's because the patterns contained in these periods are not used - we decided only to trade the index components.
With these changes, we retrained the long model, trained a short model (using the same features and process described in the last article, with the changes described above), and used both to inform our strategies.
The baseline strategy
The baseline strategy is basically what we used in our last article but with the fixes described above—trading only the Russell 3000 stocks.
At the opening of every trading session:
We will split our capital into 20 slots and buy stocks whose 3-day QPI from the previous day closed below 15, and the model we trained outputs a probability of bouncing back is above 60%;
We will have no regime filter, as we included a feature that considers the distance between the closing price and the 200-day SMA;
We will only trade Russell 3000 constituents: at any given day, the only opportunities we will consider are the stocks that belonged to the index on that day;
If there are more than 20 stocks in the universe with the entry signal triggered, we will sort them by the probability of bouncing back and prioritize the most probable moves;
We will hold 20 positions maximum at any given moment;
We use stop-loss orders (trigger at the entry price -5%) and time-limit (6 bars).
To ensure we trade only liquid stocks:
We won't trade penny stocks (whose closing price is below $1);
We will only trade the stock if the allocated capital for the trade does not exceed 5% of the stock's median ADV of the past 3 months from the day in question.
Here are the results for comparison with what we saw in our last article:
As we can see, the results are good, but not as good as we obtained in the previous article:
Annual returns are at 27.4%, over 2x the benchmark, but not even close 40%;
Sharpe ratio is at 1.17, almost twice the S&P 500, but below the 1.33 we saw previously;
Max drawdown is a bit better at 46% (vs. 50% from last week) but still well above the benchmark's 34%;
The win rate is good at 62%, about the same vs. the previous week (60.5%);
However, the expected return/trade is now at +0.5% (vs. +0.7%), with a payoff ratio of 0.79 (vs. 0.86).
Now, let's improve the strategy by adding the short leg.
Long & Short
Training the short model was straightforward:
We used the same features and same training process as described in the latest article;
On top of the changes described above (also used to retrain the long model), the only changes were: i) we collected events of stocks in upward moves, and ii) we trained the model to predict the probability of the stock to revert back down (instead of bounce back up), changing the signs/flipping the inequalities accordingly.
The strategy:
We keep the long leg exactly as described;
We introduce a short leg with 20 short positions, exactly like the long leg but in reverse, using the trained short model;
So, at any given point in time, we hold 20 long positions max and 20 short positions max;
The long portfolio has 1.1x all the available capital, while the short portfolio has 0.2x; the reduced short portfolio size is a risk management decision to protect us from shorting the wrong stocks, while the long bias efficiently allocates part of the resources generated by the short selling.
Here are the results:
Adding the short leg improved the results, as expected:
The annual return reaches 31.6%, +4ppts vs. the long-only strategy;
Sharpe ratio also increases, now at 1.24;
However, maximum drawdown also spikes, reaching 50% — too high;
Win ratio is slightly worse at 59.5% (vs. 61.7%), which is offset by a much better payoff ratio of 0.87 (vs. 0.79), leading to an expected return per trade of +0.78% (vs. +0.55%).
There's only one critical drawdown (COVID); all the others are below 20%. However, this 50% maximum drawdown during COVID bothers me. What could we do to try to protect our system from events like that?
A VIX-based regime filter
Many systems' go-to regime filter is based on how the market (usually represented by the S&P 500) closes with respect to its 200-day SMA: if it closes above the average, we consider it a bull market, while if it closes below, we consider it a bear market.
This simple regime filter works sometimes but not always. Here, let's try a different approach: a VIX-based regime filter. Here's how it is going to work:
We will compute VIX's 15-day SMA;
We will add 15% to the 15-day SMA;
If the VIX closes above the value obtained above, we will consider a bear market; otherwise, we will consider a bull market.
Now, let me explain the details of the rules above:
It's self-evident that low VIX is related to bull markets, while high VIX is related to bear markets;
We use a short SMA (15 days) because we want the filter to respond fast whenever the market goes from a bull to a bear market, as well as also fast whenever the market goes from a bear back to a bull market;
We added 15% to the 15-day SMA because, if we don't, there are too many bull-bear-bull transitions; adding this threshold ensures there are fewer transitions and that the time spent in bull/bear markets reflects the reality more accurately;
The particular choice of 15% is justified because 15% represents the 90th percentile of the % difference between VIX close and its 15-day SMA. In other words, 90% of the values of the % difference between VIX close and its 15-day SMA are below 15%; only 10% are above this level;
If we don't add this 15%, the system will be in a bull regime ~60% of the time, which does not represent what we observe in the market; adding it ensures the system is in a bull regime ~90% of the time, which is more accurate in reality.
Finally, here's how the system will behave:
In bull markets, no changes: the long portfolio will continue to be 1.1x of all available capital to trade, while the short portfolio will be 0.2x;
In bear markets, the long portfolio will become 0.1x of all available capital to trade, while the short portfolio will continue to represent 0.2x;
With this rule, we will ensure that most of our capital moves to cash during downturns (what is allocated is short-biased) and returns to fully trading our strategy when the regime turns bullish.
Let's see how this system behaves:
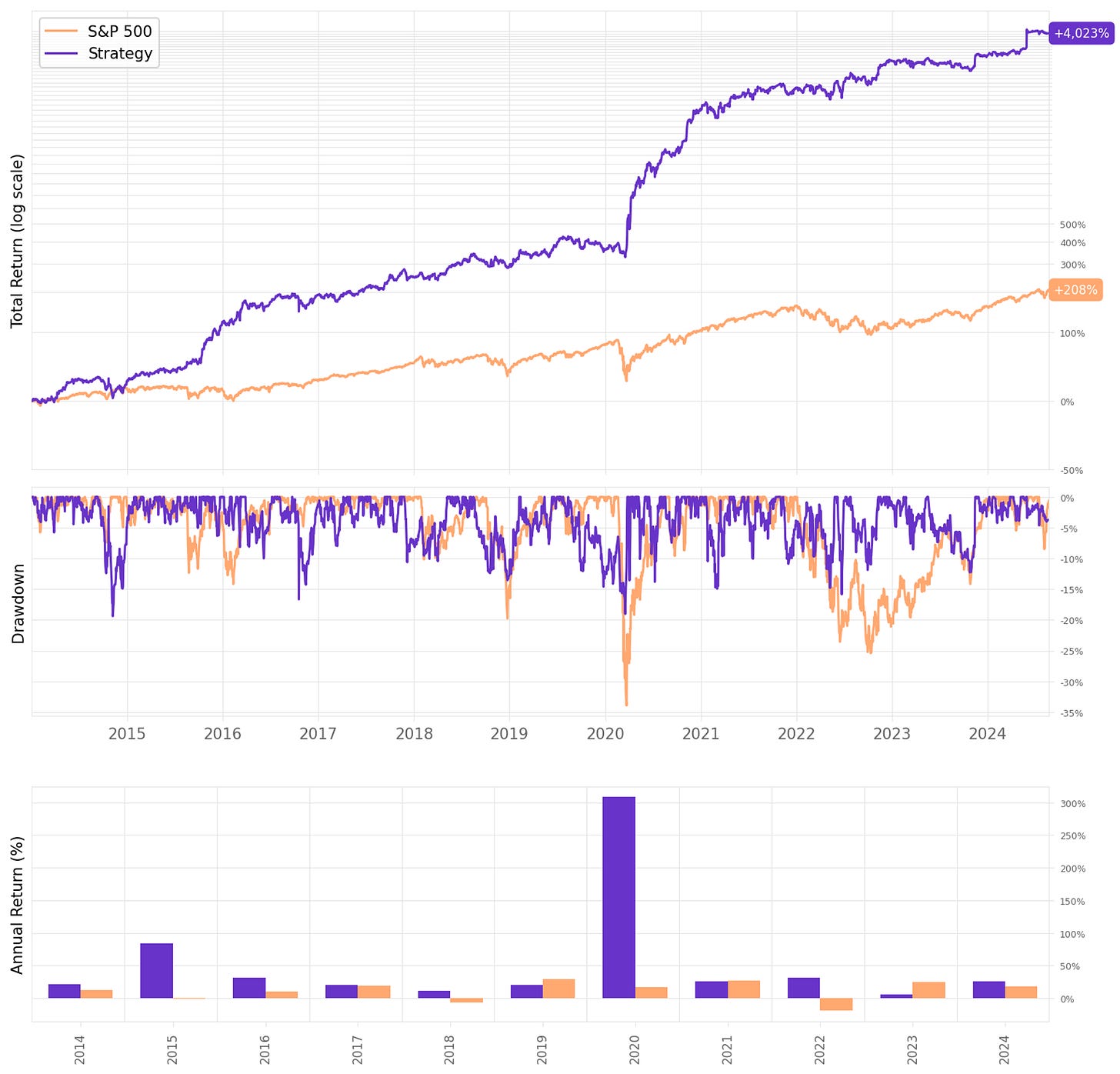
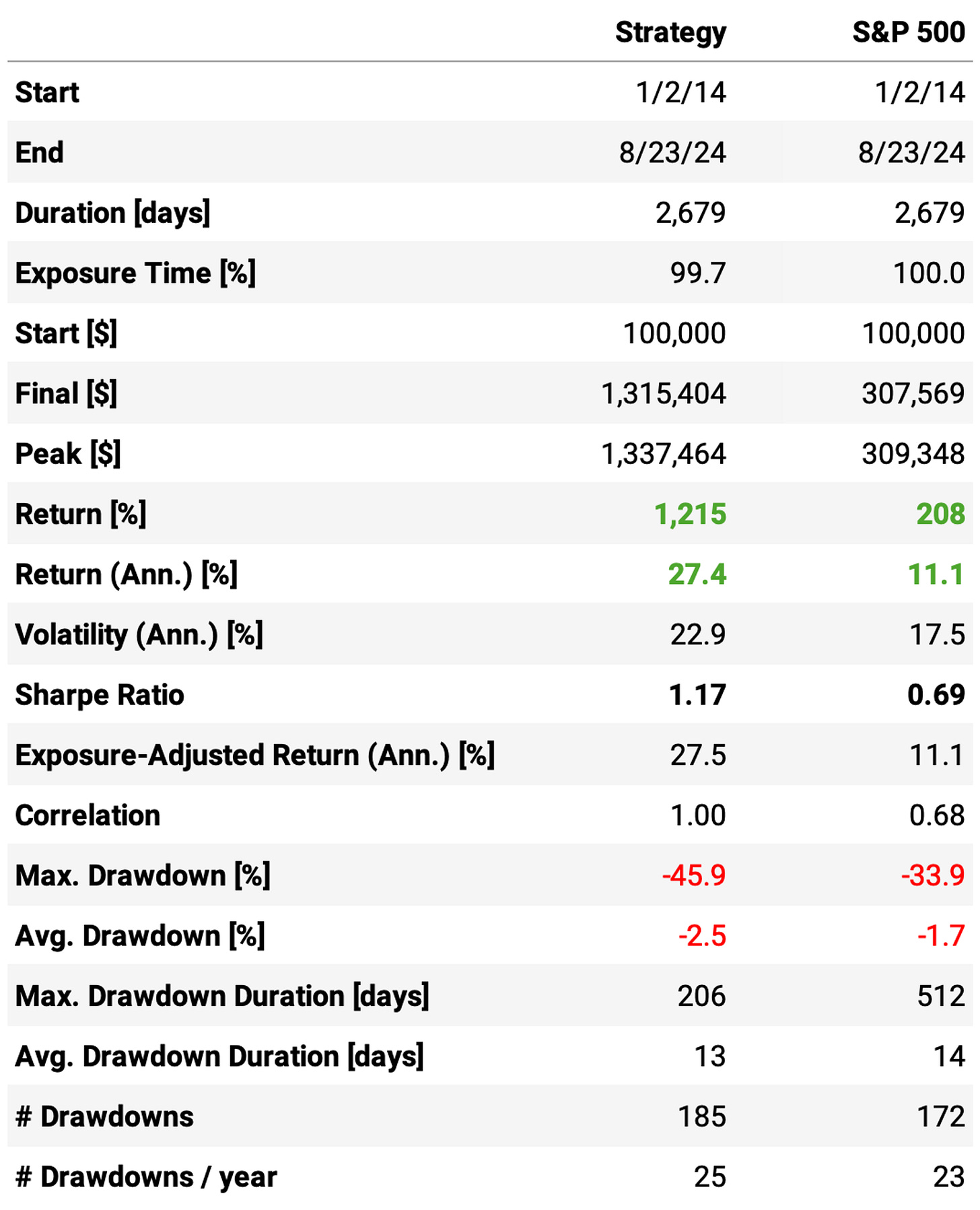
Wow! Much better results. The highlights:
The annual return is now at 41.9%, a +10ppts vs. the “filterless” system;
Sharpe ratio is 1.55, over twice the benchmark's;
Maximum drawdown has a significant reduction, now at 19%;
The trade stats continue about the same.
Let's check the monthly and annual returns:
If we had traded this strategy since 2014:
We would have had only positive years, no down years;
We would have seen 66% of the months positive, with the best at +46.8% (Mar’20);
We would have seen 34% of the months negative, with the worst at -10.0% (Apr'22);
The longest positive streak would have been 11 months, from Mar'20 to Jan'21;
The longest negative streak would have been 4 months, from Nov'19 to Feb'20.
Trading costs
The 2-basis points assumption for slippage + trading costs might not hold anymore now that we are trading stocks beyond what is present in either the S&P 500 or NASDAQ-100. So, let's see how different levels of trading costs impact the results:
Final thoughts
After I found the subtle bias and the improvement areas in the production code, I imagined I would address the issues and get more modest backtest results. Unfortunately, that's not the case: the numbers continue to look too good.
This time, however, the code has been double-checked. The triple check will come from the market results.
In fact, if we remove the 2020 spectacular year when the system surfed the COVID recovery, the annual return becomes 26%. This is more likely to be the system's real performance.
In any case, if I find any other biases or wrinkles in the code that could potentially change the results, I'll write another piece explaining what I found and how to fix it.
I'd love to hear your thoughts about this approach. If you have any questions or comments, just reach out via Twitter or email.
Cheers!










How exactly did you go about selecting the 15day SMA and 15% parameters? It would be interesting to see a 3D surface map for those 2 params against performance(sharpe,maxdd,annualreturn) across a range from 5%-25% to verify that 15 wasn't chosen from data snooping.
Great article. I especially like the VIX-based regime filter. What I don't understand is how you can get 40% annual returns and have a profit factor of 1.23. I can be dense. Am I reading that right?