Mind the gap
Can a good execution algorithm enable a 28% annual return with a 19% max drawdown?
The idea
"What we know is a drop; what we don't know is an ocean.” Isaac Newton.
Many of Isaac Newton's early theories and ideas were met with skepticism or outright failure. Newton spent years working on problems related to motion, optics, and gravity, often facing dead ends and revisions.
In fact, throughout most of his career, Newton was very loathe to publish due to his high intellectual standards and his aversion to the public controversies that publishing original ideas inevitably attracted.
I am not that worried about public controversies. Whenever I believe I have found an idea that meets my quality standards, I publish it. Also, I am not that worried about being wrong: at the end of the day, the ideas I am sharing are about models, and as George Box has said, “all models are wrong.” (But some are useful.)
Nevertheless, sometimes it takes me a few experiments, and quickly, I find something worthy of sharing by my standards. However, sometimes, it takes me a lot of failed experiments until I arrive at something. That's one of the reasons why it took me three weeks since the last article to publish this one.
This week's idea is a study on gaps. It's the first statistical investigation on how trading stocks that have shown gaps between days might be a profitable idea as long as we have a careful execution to control slippage.
There are many resources on the internet explaining all kinds of trading strategies based on gaps. A nice introduction to the topic is Scott ‘The Gap Guy’ Andrew's interview with Andrew Swanscott.
I remember hearing this interview a while ago: it sparked my curiosity, and as a result, I tried several approaches to devise a profitable gap strategy. All failed. The idea went to my “revisit later” bucket. I kept revisiting it, and eventually, over these last three weeks, I tried a specific approach that worked this time.
As usual, this is not a definitive write-up about the topic. None of my articles are. It's the first study that looks promising after looking at the data. In fact, this study seems so promising to me that I will share the overall gist but refrain from quoting specific parameters. But you can fill in the blanks as you please.
Here's the plan for today:
First, we will look into the distribution of gaps for a given stock;
Then, we will statistically prove that trading these gaps has an edge;
We will then experiment with some backtests
Finally, we will talk about execution, which is crucial to make a strategy like this work.
Distribution of gaps
First, let's take CSCO as an example. Let's look at its distribution of gaps:
As expected, we see a distribution that resembles a normal distribution centered at zero. Now, let's pick an arbitrary point on the X-axis, i.e., a maximum value, and analyze what would have happened if we had bought all events when CSCO had opened with a gap at or below this value, provided that it also had opened above its 200-day SMA, and sold at the next open:

There would have been fewer than a thousand of these events throughout history. The winning rate would have been 56%, with an expected return per trade of 0.2% overall. That's the gist of the idea.
The edge
Now, let's check the idea's overall edge. What would have happened if we had bought all events when a stock (belonging to S&P 500) had had a gap down by a particular value, provided that its opening price was above its 200-day MA, and sold at the next opening?

We see a positive expected return:
We can expect a +0.1% return/trade;
The win ratio is at 55%;
There's a slightly negative payoff ratio: the expected return on winning trades is +1.5% vs -1.6% on losing trades.
Looking at non-events (gap downs above the particular value we've chosen), we see an expected return per trade of only 5 bps and a win ratio of 52%. But most importantly, the P-value is well below 0.05: the means of the two distributions are significantly different. So, we have an edge.
Now, let's check how many stocks trigger the entry rule throughout history:
So, we have a sufficient number of stocks triggering the entry rules.
Finally, let's look at how this edge varies with volatility:
An interesting observation is that the lower the volatility, the higher the win ratio and the expected return per trade.
With this fact, we are ready to devise a strategy.
Strategy
The strategy rules are surprisingly simple:
At the openings, we will look into all bullish stocks (open price above 200-day SMA) that opened with a gap down vs. the last day's close;
For each stock, we will check if the gap is wider than a specific threshold;
We will select all stocks that open with a gap wider than the threshold;
We will hold 10 stocks maximum;
If there are more than 10 stocks, we will rank them by volatility and select the least volatile ones; if there are fewer, we will trade only the opportunities available;
We will hold these positions until the next opening when we will sell at the opening and repeat the process.
As you are probably already thinking, this strategy is pretty sensitive to slippage.
By the end of the article, we will discuss slippage in more detail and offer ideas on minimizing it.
For now, it suffices to say that we will start our experiments by considering 10 bps of slippage + trading costs (5 bps against us while buying, then another 5 bps against us when selling).
Experiments
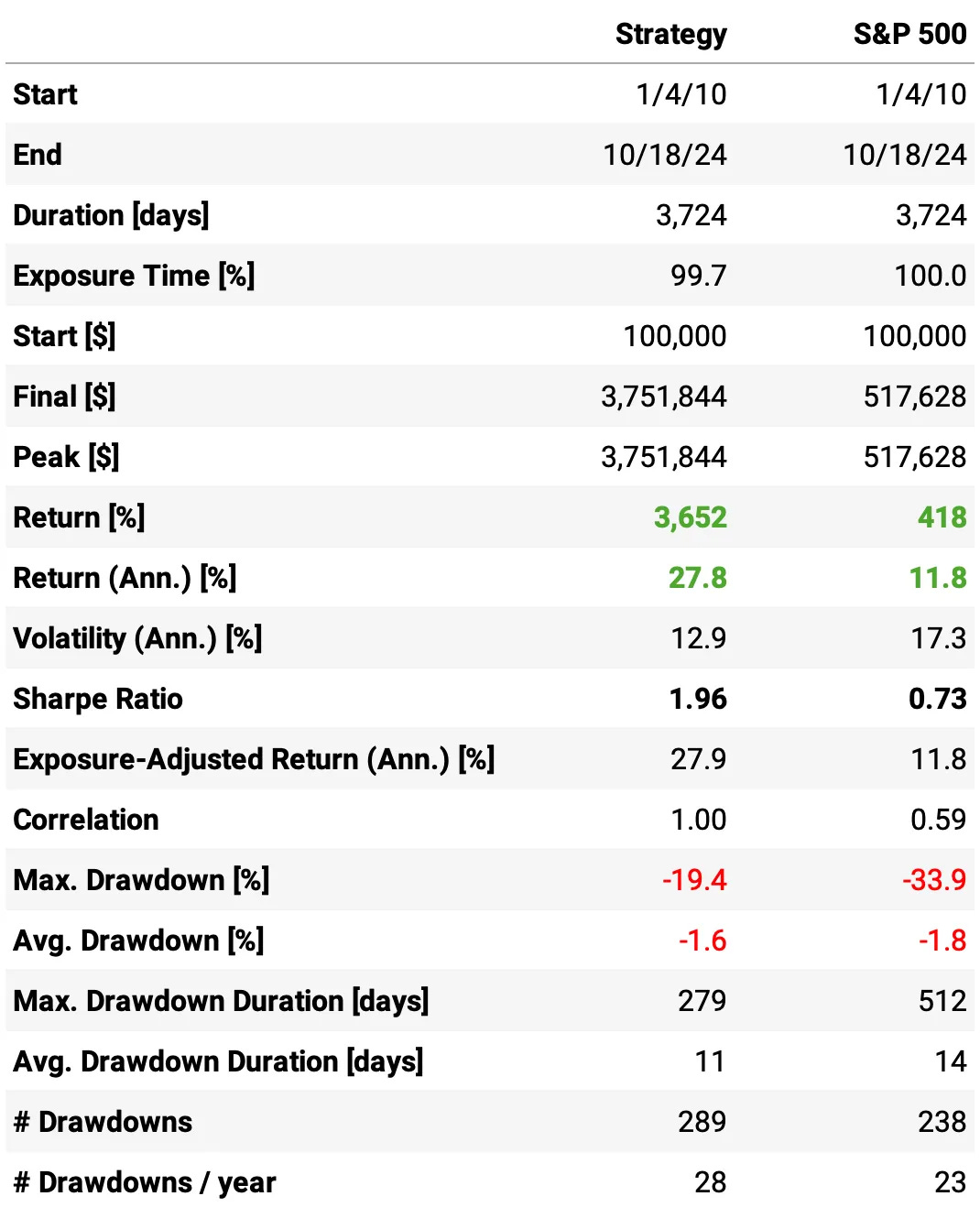
Here are the results of the first experiment. By the way, I'm only showing the results starting in 2010 because the results before 2010 were significantly better. Including them doesn't make sense, so we should focus on the more recent 15 years.
That was surprisingly positive for a first experiment:
The annual return achieved is 22.9% vs. 11.8% the S&P 500 in the same period;
The strategy was positive in 13 out of 15 years;
The maximum drawdown is at 19.7%, below what we aim (20%);
The risk-adjusted return is at 1.66 (Sharpe), vs 0.73 the benchmark;
The strategy trades 10 times/day, with a win rate of 55.6%;
The expected return per trade is +0.11%, with a payoff ratio of 0.96.
How to improve it?
Execution considerations
As we briefly discussed earlier, the execution is critical. We must minimize slippage for this strategy to work while at the same time maximizing the likelihood of filling all the orders. This can be done by:
Using limit orders instead of market orders to avoid the opening auctions;
Finding the right sweet spot time to place the orders: if we place them too fast, we increase the odds of filling all the orders; however, we end up trading suboptimal stocks (higher volatility). If we wait for too long to place the trades, we ensure selecting the best stocks to trade; however, we decrease the odds of filling all the orders;
Depending on the size of the account (we will discuss capacity in the final thoughts), we may break orders into smaller blocks.
One of the reasons it took me three weeks to publish this article instead of the usual once-a-week frequency was that I wanted to implement this execution algorithm and forward test it a bit before sharing this idea. My thought was that if I can't get less than 10 bps of slippage in the round-trip, I will place this idea back into the “revisit later” bucket.
However, I'm happy to say that, so far, the live forward tests are showing promising results for the account size I'm trading, with slippages below this threshold. Of course, that's not 100% guaranteed, as the slippage obtained is a function of how good the IBKR paper trading system is. We will only be able to say for sure that our execution algorithm that places orders is actually good at minimizing slippage with live trading. I will write about it once I have live trading data—one step at a time.
So, let's just show two more simulations:
One worse, with 12 bps;
One better, with 8 bps.
Let me highlight again: these results are only indicative. They are dependent on:
The execution algorithm each trader uses, with their unique logic details about how to place the orders;
The account size (more on capacity later).
12 bps of slippage
Here are the indicative results if the execution algorithm that places the orders manages to achieve a total of 12 bps of slippage per trade (6 bps when buying + 6 bps when selling):
8 bps of slippage
Here are the indicative results if the execution algorithm that places the orders manages to achieve a total of 8 bps of slippage per trade (4 bps when buying + 4 bps when selling):
Final thoughts
This is the first study on gap mean reversion and slippage. The first backtests are appealing enough to drive further investigation, and the early results from the forward test also corroborate.
After a few weeks of forward tests, once we have a sufficiently large sample size of trades, if we verify the trade stats closely resemble what we saw on the backtests, we should move to live trading. If that happens, we should start small and grow from there.
Assuming that it works, we should then ask ourselves: what is the capacity of a strategy like this? I would guess up to a few million, maybe even low tens of millions. But for sure, it has a number above which the returns rapidly decrease. Otherwise, large funds would have already arbitraged out this type of idea.
The only way to know for sure is live trading. However, an idea to estimate the capacity is to analyze the volume % of each stock traded at or below the opening price in the first minutes of the day. This can be done by collecting trade-by-trade market data from IBKR for a few weeks. But that comes down the road iff i) the forward test finishes with a positive outlook and ii) the live trading with a small account delivers the expected returns. If everything works out, this might be a good idea for small funds/family offices.
I'd love to hear your thoughts about this approach. If you have any questions or comments, just reach out via Twitter or email.
Also, if you want to implement this strategy (or any other strategy) and need help, just let me know.
Cheers!















What backtesting library you are using?
how big of a gap down at open was the test?