A Mean Reversion Strategy from First Principles Thinking
Using a problem-solving technique to deliver 24% annual return trading S&P 500 constituents

The idea
“I think it’s important to reason from first principles rather than by analogy. The normal way we conduct our lives is we reason by analogy. [With analogy] We are doing this because it’s like something else that was done, or it is like what other people are doing. [With first principles] you boil things down to the most fundamental truths… and then reason up from there.” Elon Musk.
What does Elon Musk, Aristotle, Richard Feynman, Thomas Edison, Albert Einstein, Steve Jobs, Nikola Tesla, Charlie Munger, Leonardo da Vinci, Benjamin Franklin, Claude Shannon, and Rene Descartes, among other of the greatest thinkers and innovators who ever lived, had in common?
They are all known for embodying “First Principles Thinking” in their work and approach to problem-solving.
First Principles Thinking is like creating an original song from basic notes rather than being in a cover band that plays existing songs. It involves breaking down a problem into its fundamental components and building something new from scratch instead of replicating what has already been done.
First Principles Thinking can be traced back to the ancient Greek philosopher Aristotle. Elon Musk recently popularized this problem-solving technique, as he used it to reduce the cost of space travel dramatically.
In general, this is the step-by-step guide on how to apply First Principles Thinking to solve problems:
Identify the Problem;
Break Down the Problem;
Challenge Assumptions;
Identify First Principles;
Rebuild the Problem from First Principles;
Test and Iterate.
This week, we will build a profitable mean reversion strategy using First Principles Thinking. Here's the plan:
First, we will deconstruct a mean reversion strategy into its basic components and question the assumption of RSI-2 as the default indicator of mean reversion in stocks;
Then, we will rethink what deviation from the mean is in terms of its foundational elements - probabilities - and use them as building blocks to create an indicator to trigger entry signals;
We will statistically prove that this invented indicator has an edge;
Finally, we will show how this new indicator can be used to inform a strong mean reversion strategy through a series of backtests.
Deconstructing a mean reversion strategy
Let's break down a mean reversion strategy into smaller, more manageable parts:
Entry trigger. Every mean reversion strategy has a set of entry rules that, when triggered, tell us to go long (or short) if the instrument's price has deviated down (or up) from the mean.
Exit trigger. Also, every mean reversion strategy has a set of exit rules that, when triggered, tell us to close the position.
So far, we have been using the Relative Strength Index (RSI) to inform us when to enter mean reversion trades. To exit, we generally either also use the RSI or a simple set of rules such as:
The closing price is higher than yesterday's high (which indicates the reversion is completed);
Time (number of bars since the trade started).
The Relative Strength Index (RSI) is a momentum oscillator that measures the speed and change of price movements. It was developed by J. Welles Wilder and popularized in mean reversion strategies by the work of Larry Connors and Cesar Alvarez. Their research showed that using RSI with a short window (2 days) delivers an edge, which can be profitably exploited. Strategies based on the 2-day RSI have worked well throughout the past decades.
Usually, we take a long (or short) position whenever a stock's 2-day RSI falls below (or reaches above) a threshold such as 10 (or 90) and hold the position until the exit rule is triggered.
Thinking in terms of probabilities
Is the RSI the best mean reversion indicator to inform the entry signal, or is it just an accepted norm? What is a deviation from the mean?
Let's think in terms of probabilities:
Imagine a stock from a company with solid fundamentals, whose fundamentals are unlikely to change overnight;
For a stock like this, we could say the larger the short-term price drop, the more probable this stock's price is to bounce back;
So, the probability of an event of a price drop of that magnitude or higher is the basic element upon which we should create an indicator to inform the entry signal!
Let's illustrate that with an example. On Jan-21, 2022, Apple stock had accumulated a 3-day price drop of -4.4%. This is rare. On that day, if we looked back 5 years, this would be the 3-day returns distribution for Apple stock:
The probability of a drop of that magnitude or higher, given it was a drop, is the area of the red region in the histogram divided by the area of the histogram at the left of zero. This value is 10.7% and represents how rare an event like this is.
Not surprisingly, if we had bought Apple stock at the next open and held it for 5 days, we would have profited +6.4%.
Now, let's look at an example in the short side. On Nov 2nd, 2023, Tesla stock had accumulated a 3-day price surge of +10.7%. This is also rare. On that day, if we looked back 5 years, this would be the 3-day returns distribution for Tesla stock:
The probability of a surge of that magnitude or higher, given it was a price increase, is the area of the red region in the histogram divided by the area of the histogram at the right of zero. This value is 11.7%, and it represents how rare an event like this is.
Also not surprisingly, if we had sold Tesla stock at the next opening and covered the position 5 days later, we would have profited +5.1%.
The QP indicator and its edge
For the lack of a better name, let's call this indicator QP (Quantitativo's Probability). It indicates how probable a price change of that magnitude or more extreme is, in a window of N days, looking back at Y years from the date in question.
Let's set a default window N of 3 days, as we want to capture short-term mean reversion, and a default look back of 5 years to retrieve the 3-day returns histogram. So, to compute the QP indicator for the stock S on a given date:
We look back 5 years from the given date and get all 3-day returns in this period;
Then, we get the percentile of the 3-day price change on the given date if the 3-day price change is negative (or 100 minus the percentile if the 3-day price change is positive);
Finally, we divide this value by the area at the left of the zero in the histogram if the 3-day price change is negative (or at the right if it is positive) and multiply by 100.
That's it. This number will vary between 0 and 100. The closer it is to zero, the rarer the event. The closer it is to 100, the more common the price change.
Now, let's check QP's edge. What would have happened if we had bought all events when a stock had had a price drop, when its 3-day QP indicator was below 15, with its closing price above its 200-day simple moving average (stock in an upward trend), and held it for 5 days?

We see a positive expected return:
We can expect a +0.6% return/trade
The win ratio is at 55%
There's a positive payoff ratio: the expected return in winning trades is +4.6%, vs -4.3% on losing trades.
Now, let's look at non-events. We define non-events as buying stocks whose 3-day QP is above 15, with all other conditions the same as the events.
Here, we see worse stats: the expected return per trade is +0.3%, half of what we saw on the events, while the win rate is slightly worse as well.
But most importantly, the P-value is well below 0.05: the means of the two distributions are significantly different. So, we have an edge.
Now, let's check how many stocks trigger the entry rule (i.e., have their QP indicator below 15) throughout history:
So, we reconstructed our understanding of a mean reversion strategy, rethinking the entry signal in terms of probabilities rather than the commonly used RSI. This led to the creation of a new indicator, which we called the QP indicator. Now, let's see how useful this indicator is.
The strategy
The strategy we will trade is actually pretty simple. At the opening of every trading session:
We will split our capital into 10 slots and buy stocks whose 3-day QP indicator from the previous day closed below 15;
We will only trade stocks whose price closed above its 200-day simple moving average;
If there are more than 10 stocks in the universe with the entry signal triggered, we will sort them by turnover and prioritize the most liquid ones;
We will hold 10 positions maximum at any given moment.
When the stock closes above yesterday's high, we will exit on the next open.
We will only trade S&P 500 constituents. The test does not have either survivorship bias or selection bias. We use Norgate data (S&P 500 Current & Past).
That's it. Let's see how this strategy performs.
Experiments
We start by backtesting the strategy exactly as defined above:
Wow! That was surprisingly positive for a first experiment:
The annual return achieved is 15.5% vs. 8.5% the S&P 500 in the same period;
The strategy was positive in 21 out of 22 years;
The maximum drawdown is at 30%, about half of the benchmark;
The risk-adjusted return is at 0.93 (Sharpe), vs 0.53 the benchmark;
The strategy trades 399 times/year, or about 7-8 times/week, with a win rate of 65.5%;
The expected return per trade is +0.39%, with a payoff ratio of 0.71.
How to improve it?
Reducing the number of slots
Instead of trading 10 instruments in parallel, let's reduce the number of slots to 4.
The highlights:
The annual return increased to 19.9%, over twice the benchmark;
The Sharpe ratio also increased, now reaching 0.98;
The maximum drawdown remained about the same, at 31%, vs. 57% the S&P 500;
The number of trades/year dropped by more than half, now at 187 (3-4/week).
What else could we do to improve it?
Long & short
Now, let's add a short leg to the strategy. It will work exactly as the long, but in reverse. The QP indicator threshold for going long or short will be 15. The difference between long and short is that:
Long opportunities are stocks whose price dropped in the past 3 days, whose QP is below 15 (i.e., the probability of a price drop of that magnitude or higher is 15%), and whose price has closed above its 200-day simple moving average;
Short opportunities are stocks whose price surged in the past 3 days, whose QP is also below 15 (i.e., the probability of a price increase of that magnitude or higher is 15%), and whose price has closed below its 200-day simple moving average;
Additionally:
For longs, we will continue with 4 slots as the maximum number of positions we will hold in the long portfolio at any given moment;
For shorts, we will set 12 slots as the maximum number of positions we will hold in the short portfolio at any given moment. That's because we want more diversification in the short side to protect ourselves from outliers;
We are sorting opportunities by turnover and restricting ourselves to trade S&P 500 constituents. This means we will be going long and short for the largest stocks in the market. To increase our protection on the short side even further, we will make the short portfolio 15% the size of the long portfolio.
Now, let's see how these rules perform:
Another significant improvement:
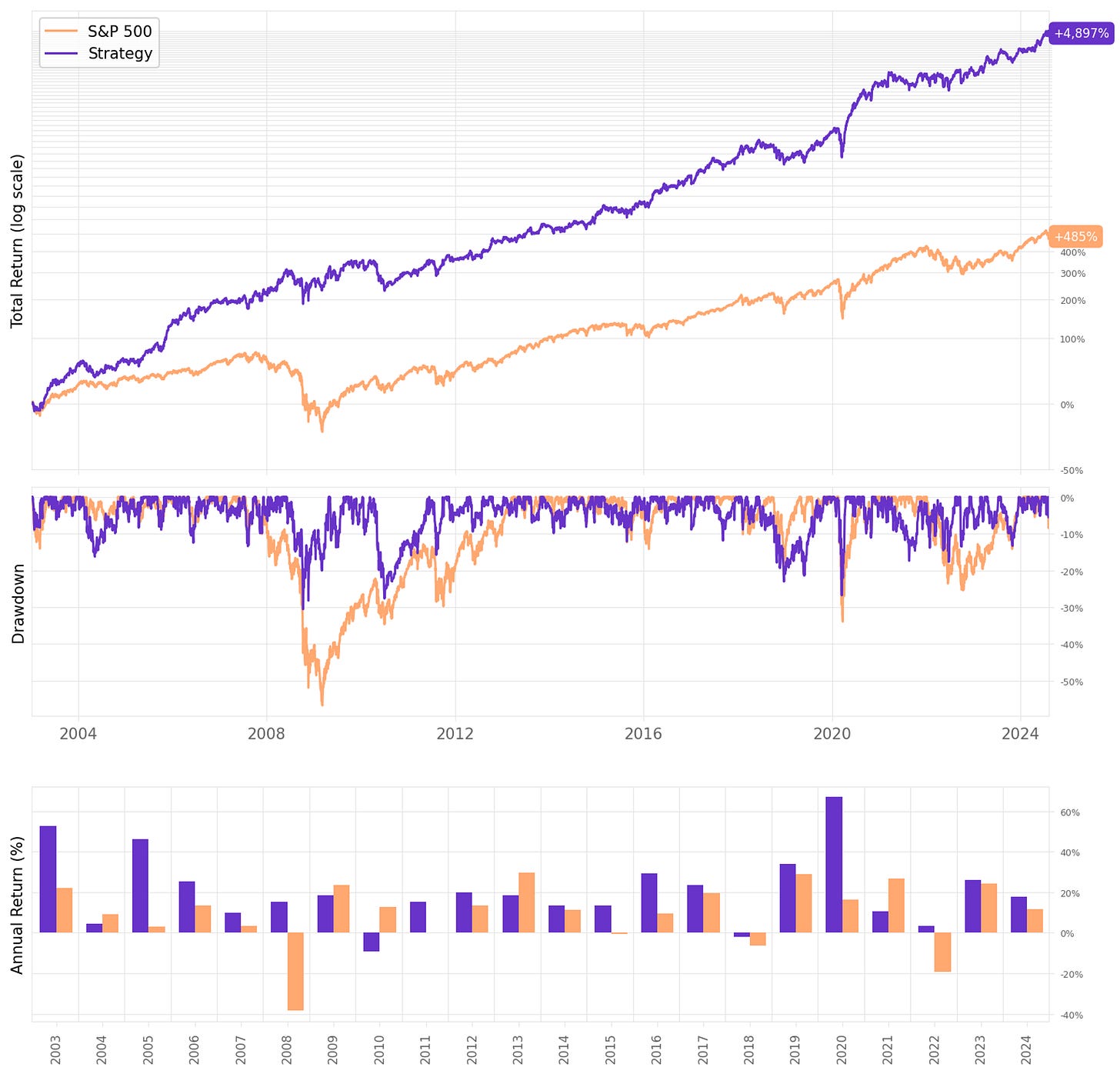
We achieved a 23.9% annual return, about 3x the benchmark;
Sharpe ratio increased to 1.10, over twice the S&P 500;
Maximum drawdown reduced from 30% in the previous experiments to 26%, less than half the benchmark;
The average return/trade increased to +0.65%;
The win rate slightly decreased to 64%, while the payoff ratio improved to 0.81;
However, adding a short portfolio with 12 slots significantly increased the # of trades/year, now at 888 in total (about 17 trades/week, or 3-4 trades/day).
Let's see the returns month by month:
If we had traded this strategy since 2023:
We would have had only 1 down year in 22 years (2010);
We would have seen 64% of the months positive, with the best at +21.4% (Sep’11);
We would have seen 36% of the months negative, with the worst at -11.2% (Jun'10);
The longest positive streak would have been 9 months, from Feb'03 to Oct'03;
The longest negative streak would have been 6 months, from Apr'21 to Sep'21.
Trading costs
Finally, let's check the impact of trading costs on the results:
As expected, the higher the trading costs, the lower the returns.
Final thoughts
First Principles Thinking is a powerful problem-solving approach. When applied to rethinking a mean reversion strategy, it enabled the creation of a completely new indicator from fundamental elements, resulting in an effective and profitable strategy.
Should we trade this strategy as is? Hold your horses. There are improvements to be made in this strategy such that we get a better win ratio and a better payoff ratio. In fact, this strategy is the first step of a larger vision, to be shared with time. Baby steps. :)
I'd love to hear your thoughts about this approach. If you have any questions or comments, just reach out via Twitter or email.
Also, if you want to implement this strategy (or any other strategy) and need help, just let me know.
Cheers!














Instead of doing short, can we apply market regime filter (for instance based on ATR or similar)?
I'm trying to replicate your results again, but this code is definitely more complex. I would appreciate it if you could explain the logic used to optimize the code for testing the 10 slots. I imagine you didn't test the conditions for each of the 500 S&P stocks for every trade. I created a vector with the top 50 and ran the backtest, but the results were different. Thanks!